Adjacent Angles | What Are Adjacent Angles?

Adjacent Angles: In plane geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays lie in a plane, but this plane does not have to be a Euclidean plane. Angles are also formed by the intersection of two planes in Euclidean and other spaces. These are called dihedral angles. Angles formed by the intersection of two curves in a plane are defined as the angle determined by the tangent rays at the point of intersection. Similar statements hold in space, for example, the spherical angle formed by two great circles on a sphere is the dihedral angle between the planes determined by the great circles.

Angle is also used to designate the measure of an angle or of a rotation. This measure is the ratio of the length of a circular arc to its radius. In the case of a geometric angle, the arc is centered at the vertex and delimited by the sides. In the case of a rotation, the arc is centered at the center of the rotation and delimited by any other point and its image by the rotation.

The word angle comes from the Latin word angulus, meaning “corner”; cognate words are the Greek ἀγκύλος (ankylοs), meaning “crooked, curved,” and the English word “ankle”. Both are connected with the Proto-Indo-European root *ank-, meaning “to bend” or “bow”.

Adjacent Supplementary

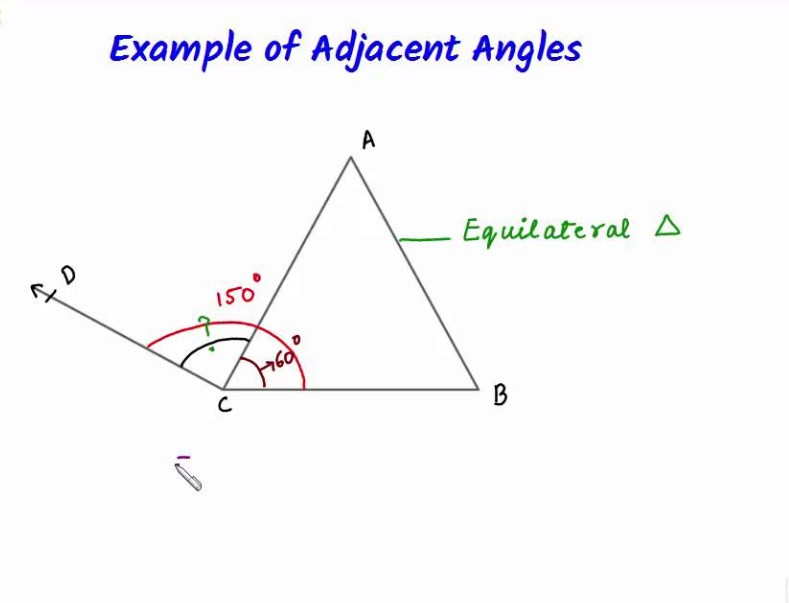
Adjacent are two angles that have a common vertex and a common side. The vertex of an angle is the endpoint of the rays that form the sides of the angle. When we say common vertex and common side, we mean that the vertex point and the side are shared by the two angles. Here’s an example of adjacent :

Adjacent
In this diagram, point A is the vertex of all of the angles shown. Angle DAJ and angle JAT are adjacent because the red ray AJ forms a side of each of those angles.

 

You can think of adjacent as two pizza slices next to each other in the box. The corners of the slices are both at the center of the box; that’s where the vertex is. The cut where the slices were separated from one another is the side the angles share.

In the whole pizza, there are several other pairs of adjacent . Every angle can have two possible different angles adjacent to it, one attaching to each side of it. Using our pizza slices, if you have three slices of pizza, the middle piece has two pieces that are adjacent to it. Just remember that adjacent refers to two degree at a time.

Identifying Degree

In mathematical expressions, it is common to use Greek letters (α, β, γ, θ, φ, . . . ) to serve as variables standing for the size of some angle. (To avoid confusion with its other meaning, the symbol π is typically not used for this purpose.) Lower case Roman letters (a, b, c, . . . ) are also used, as are upper case Roman letters in the context of polygons. See the figures in this article for examples.

Potentially, an angle denoted, say, ∠BAC might refer to any of four angles: the clockwise angle from B to C, the anticlockwise angle from B to C, the clockwise angle from C to B, or the anticlockwise angle from C to B, where the direction in which the angle is measured determines its sign (see Positive and negative angles). However, in many geometrical situations it is obvious from context that the positive angle less than or equal to 180 degrees is meant, and no ambiguity arises. Otherwise, a convention may be adopted so that ∠BAC always refers to the anticlockwise (positive) angle from B to C, and ∠CAB to the anticlockwise (positive) angle from C to B.

Linear Pair

What is the sum of adjacent ? The adjacent will have the common side and the common vertex. Two angles are said to be supplementary if the sum of both the angles is 180 degrees. If the two supplementary are adjacent to each other then they are called linear pair.

Sum of two adjacent supplementary = 180^o.

Pair of adjacent whose measures add up to form a straight angle is known as a linear pair. The angles in a linear pair are supplementary.

Consider the following figure in which a ray OP- stand on the line segment AB   as shown:

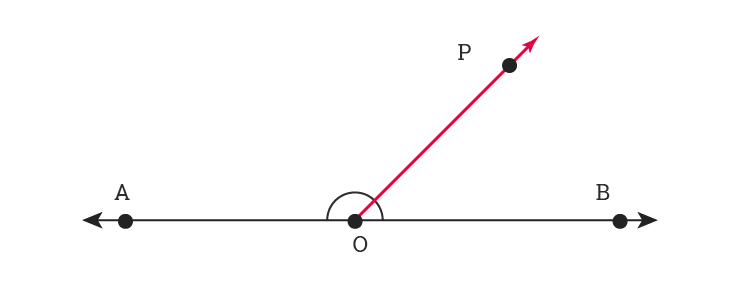
The angles ∠POB and ∠POA are formed at O. ∠POB and ∠POA are adjacent and they are supplementary i.e. ∠POB + ∠POA = ∠AOB = 180°

∠POB and ∠POA are adjacent to each other and when the sum of adjacent angles is 180° then such angles form a linear pair of angles.