You may have already seen graphs with similar shapes but different widths. The functions may have been horizontally stretched using a base function. The horizontal stretch is one of the most commonly used transformation techniques when graphing functions, so it’s best to understand its definition.

A horizontal stretch occurs when a base graph is widened along the x-axis and away from the y-axis.

We can understand the family of functions’ graphs by stretching graphs horizontally. Based on the scale factor applied, we can also learn how to graph new functions more quickly.

What is a horizontal stretch? 

We can practice horizontal stretch to a function by multiplying its input values by a scale factor, a, where 0 < 1/a < 1. What does that mean for functions like f(x)? When 1/a is multiplied to x, f(x)’s graph stretches horizontally through a scale factor of a.

Let’s go ahead and look at how f(x) = x² will be hit by a scale factor of 1/2 and 1/3.

As we have assumed, the graph stretches by a factor of 2 and 3. Notice how the y-values remain the same? This is true for all horizontal stretches. The graph only stretches away from the y-axis when we stretch it horizontally.

Other functions will exhibit similar properties to horizontal stretch. Let’s assume we have f(x) = |x|, if this function’s graph is to be stretched horizontally to attain g(x), the new function’s expression can be expressed as |1/3 ∙ x| = |x/3|.

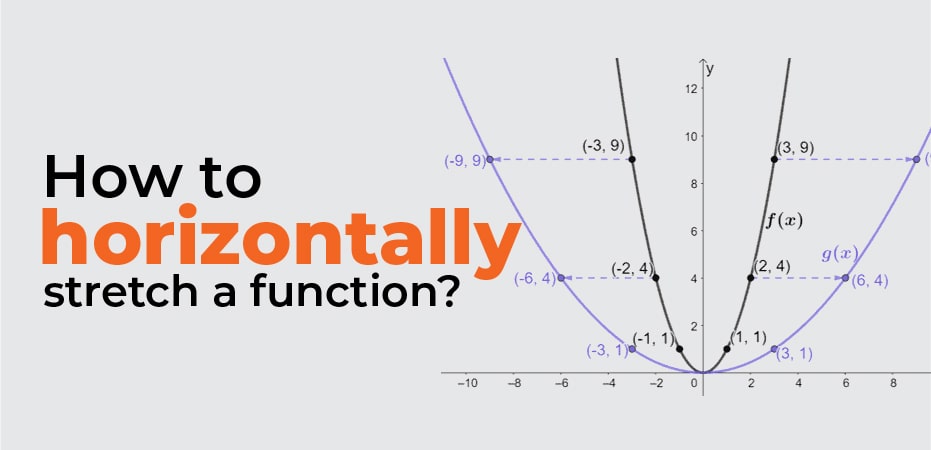
How to horizontally stretch a function?

Now that we understand how horizontal stretches affect a base function, we can apply them to function graphs. Here are a few pointers to stretch graphs horizontally faster before we start stretching functions horizontally by a certain factor:

• Extend only the base of the graph horizontally so that the y-coordinates remain the same.
• Since the y-coordinates remain the same, the y-intercept also remains the same.
• Verify critical points on the graph, such as its intercepts, maximum points, and more.
• Make sure the coordinate points are scaled correctly.

Let’s use the table of values shown in the prior section to graph both y = |x| and y = |x/3| to visualize the effects of a horizontal stretch on a graph.

As we have explained, we’re expecting the graphs to stretch along the base with the values for y remaining constant.

To attain y = |x/3|, we stretch the parent function y = |x| by a factor of 3. The graph shown above confirms this, and we can apply the same approach when horizontally stretching the graphs of other functions.

Are you ready to graph more functions and apply horizontal stretches? Before we try out more questions, let’s take a moment to summarize what we’ve learned thus far.

Summary of horizontal stretch definition and properties

In answering problems and graphing functions with horizontal stretches, it is important to remember the following:

• A graph can only be horizontally stretched by 1/a if the input value is also increased by a.
• Multiply the x-coordinates by a when f(x) is stretched horizontally to f(ax).
• Retain the y-intercepts’ position.
• As a result, the resulting function will have the same range, but a different domain.
• When a point (m, n) is stretched horizontally, it becomes (am, n).

When in doubt, let’s always refer to these five-pointers. By mastering the technique of stretching graphs horizontally, we can plot functions more quickly and understand their behavior better.

Are you ready to test your knowledge? Here are some questions for you to try out!

Example 1

The function, g(x), is obtained by horizontally stretching f(x) = 8x by a scale factor of 1/4. Choose the correct expression for g(x).

1. g(x) = 32x
   b. g(x) =16x
   c. g(x) = 2x
   d. g(x) =1/2 x

Solution

When we stretch a function horizontally by 1/a, we divide the input value by a. Why don’t we apply that to the problem? We replace x with x/4 to find the expression for g(x).

g(x) = 8(x/4)

Simplifying the expression will lead to g(x) = 2x.

Example 2

Write the expressions for g(x) and h(x) in terms of f(x) given the following conditions:

5. The function g(x) is the result of f(x) being stretched horizontally by a factor of 1/5.
   b. When we horizontally stretch g(x) by a scale factor of 1/2, we obtain h(x).

Solution

Let’s start with g(x). We can horizontally stretch f(x) to obtain g(x), so we divide the input value of f(x) by 5 to obtain g(x)’s expression: f(x/5).

Now that we have g(x), we can find the expression for h(x). We divide g(x)’s input value by 2. Hence, we have:

h(x) = g(x/2)

= f(x/5 ·1/2 )

= f(x/10)

This means that in terms of f(x), g(x) = f(x/5) and h(x)= f(x/10).

Example 3

The function, f(x), passes through the point (6, 4). What would be the new x-coordinate of the point if f(x) is horizontally stretched by a scale factor of 1/2?

Solution

When we stretch a graph horizontally, we multiply the base function’s x-coordinate by the given scale factor’s denominator to find the new point lying along the same y-coordinate.

Hence, we have (6, 4) → (2 ∙ 6, 4). The new x-coordinate of the point will be (12, 4).