How to find displacement? Displacement is often used as an alternative to distance. But, in reality, displacement and distance are two different things. Aside from displacement, in this topic, we will discuss displacement, the displacement formula, its derivation, and solved examples.

Displacement

When an object travels a distance in a particular direction in a reference frame, this is known as displacement. In simple words, when an object covers a distance in a particular direction, this is referred to as displacement.

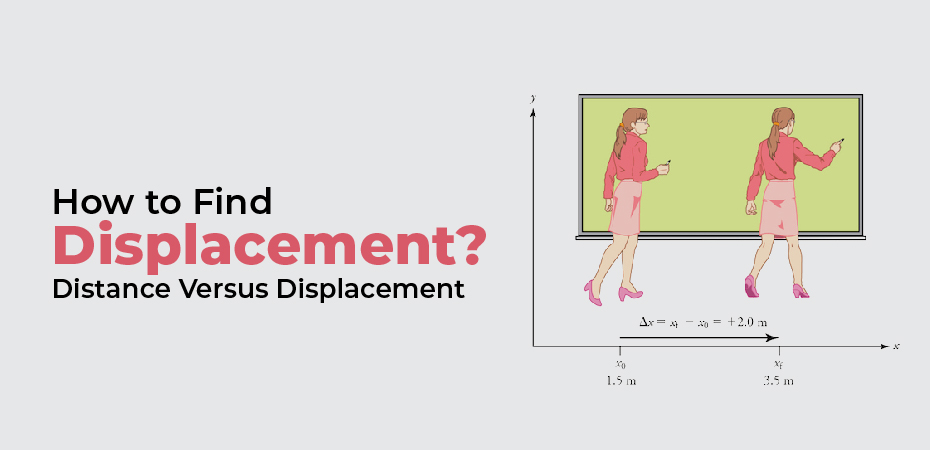
Also, displacement causes the position of the object to change. For example, movement of the car in a straight line, walking off a professor from one corner of the blackboard to another, movement of a passenger in a train or airplane, etc.

Moreover, we can define displacement as a change in the position of an object. Also, we can define it mathematically. Moreover, displacement is a vector, which means that it has a direction as well as a magnitude. It is represented visually as an arrow that points from the initial position to the final position.

Most importantly, in 1D (1 dimensional) motion, we can specify direction with a minus or plus sign. Furthermore, in order to begin a problem, it is necessary to determine which direction is positive. Usually, the positive has either a right or upward direction. However, no fixed criteria, so choosing a positive can be done in any direction.

Displacement Formula

An object’s displacement is the change in its position from its initial position to its final position. Additionally, it is a vector quantity, which means that it has both a direction and a magnitude. Furthermore, it has no S.I unit so we can measure it in meters, miles, kilometers, feet, yards, etc.

Displacement = Final position – initial position = change in position.

D = X_{f} – X_{i} = \Delta X

Derivation of Formula to Find Displacement 

D = refers to the displacement of the object
X_{f} = refers to the final position of the object
X_{i} = refers to the initial position of the object
\Delta X = refers to the change in position of an object

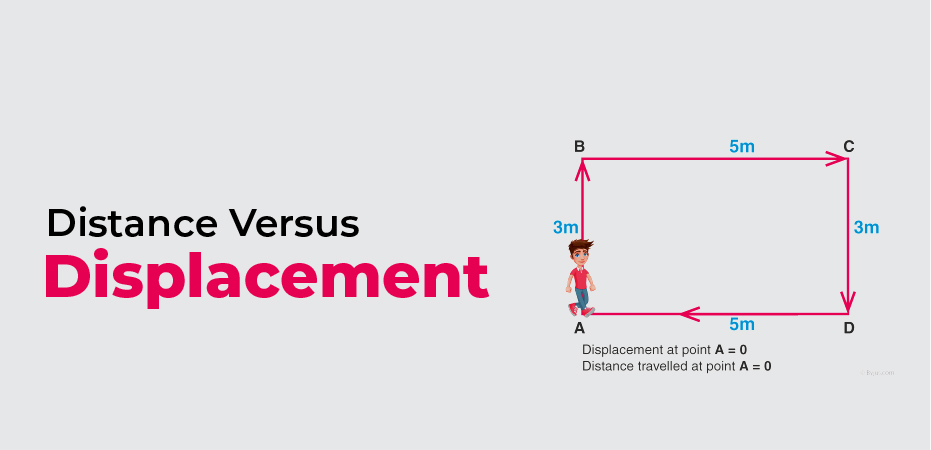
Distance Versus Displacement

Let’s start by describing these two terms, starting with the easier of the two. Distance is how much ground is covered by an object, yet of its starting or ending position. There is no directional element to distance measurement, making it a scalar quantity. So, during my 5K, I ran 5 kilometers count. It doesn’t matter where the starting line or finish line was or in which direction I was jogging. It only matters that, if you outline and measure my path, I covered a distance of 5 km of ground. So, when we asked the different runners how far I had traveled, they all answered correctly with a distance measurement of 5 kilometers.

Let’s take a minute to look at our other term: displacement, which is an entity change in position considering its starting position and final position. A displacement measure does not take into account what route the object took to change position, only where it started and where it ended. It is most straightforward to picture displacement by locating where the object started and drawing a straight arrow from this point to the point where the object stopped moving. Reflect, in physics, this arrow is called a vector. Its size corresponds to the magnitude, or size, of the movement, and the arrow points in the direction of travel. This makes displacement a vector quantity because it incorporates both movements, magnitude, and direction.

In the shorthand of physics, displacement is noted as Δs. ‘Delta’ is a Greek letter shaped like a triangle and it’s used to mean ‘change in.’ The ‘s’ stands for spatial location. So Δs stands for a shift in spatial location. You should get comfortable using this shorthand just in case you see queries asking for you to solve for Δs that don’t actually ask for displacement by name.

Solved Example on Displacement Formula

Example 1

Suppose roger leaves city A to visit steve in city B. Also, she traveled through the train, and first of all, she travels 350 kilometers to the north. But, then the track turns back to south 125 kilometers. Calculate roger’s total displacement using the displacement formula?

Solution:

The initial position of roger is X_{i} = 0 and her final position X_{f} is the distance she traveled towards the north minus the distance she traveled towards the south. So, now put the values in the equations

D = X_{f} – X_{i} = \Delta X
D = (350 km N – 125 km S)
D = 225 km N

So the total displacement of the roger is 225 kilometers towards the north.

Example 2

Think you throw a ball 25 feet north of your dog and ordered him to fetch the ball. After picking up the ball he brings it past you to your brother, who is standing 5 feet south to you from where you are standing. So, find the displacement of the ball?

Solution:

The initial position of the ball is X_{i} = 0 feet. Moreover, displacement is a vector quantity and direction is considered. X_{f} = (30 feet S – 25 feet N), So the X_{f} = – 5 feet south.

Putting values in the formula

D = X_{f} – X_{i} = \Delta X
D = (30 ft – 25 ft)
D = 5 ft

The displacement of the ball is 5 ft south of the initial position.

FAQs

Q: A car accelerates from 8m/s to 16m/s in 10m/s. What is displacement?

A: You’ll need to know the distance first. After you find it, use the equation Displacement = 1/2(initial velocity+ final velocity) • time.

Q: How can I calculate the displacement of circular objects?

A: Displacement refers to an objects change in position so in case an object moves a complete circle (360 degrees) it will not have any displacement for a noncomplete circle it is easy to discover the distance by using the below formula. Chord length = 2√(r^2 – d^2) where, r = radius of the circle d = perpendicular distance from the chord to the circle center. The chord of a circle is a line segment whose ends lie on the circle.

Q: If a man walks 1 km due east and then 1 km due North, how can I calculate his displacement?

A: You can calculate it by using this formula: S=√x²+y² (S=displacement). Plugin the given direction to the formula √1²+1² then answer it according to PEMDAS. First, is the exponent. 1 time 1 is obviously 1 so the expression should look like this now √1+1. 1+1 is 2 so this is left √2. You can either leave the answer like that or use a calculator to find the square root of 2.